Un matemático australiano ha descubierto lo que puede ser el ejemplo más antiguo conocido de geometría aplicada, en una tablilla de arcilla babilónica de 3,700 años de antigüedad, data del período babilónico antiguo entre 1900 y 1600 a. C. y fue descubierta a fines del siglo XIX en lo que hoy es Irak. Se había alojado en el Museo Arqueológico de Estambul antes de que el Dr. Daniel Mansfield de la Universidad de Nueva Gales del Sur (UNSW) lo rastreara.
Conocida como Si.427, la tableta tiene un plano de campo que mide los límites de algunas tierras.
Mansfield y Norman Wildberger, profesor asociado de la UNSW, habían identificado previamente otra tableta babilónica que contenía la tabla trigonométrica más antigua y precisa del mundo. En ese momento, especularon que era probable que la tableta hubiera tenido algún uso práctico, posiblemente en topografía o construcción.
Esa tableta, Plimpton 322, describía triángulos en ángulo recto usando triples pitagóricos: Un triple pitagórico se ajusta a la ecuación a2+b2=c2, donde los lados que definen un triángulo que son adyacentes al ángulo recto son ayb, y la hipotenusa (el lado más largo) es c. El ejemplo más simple sería 32+ 42= 52.
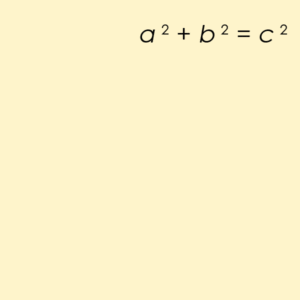
“No se te ocurre la trigonometría por accidente, por lo general estás haciendo algo práctico”, dijo Mansfield. Plimpton 322 lo puso en una búsqueda para encontrar otras tabletas del mismo período que contenían triples pitagóricos, lo que finalmente lo llevó a Si.427.
“Si.427 se trata de un terreno que se está vendiendo”, dijo Mansfield. En escritura cuneiforme, con sus características hendiduras en forma de cuña, la tablilla describe un campo que contiene áreas pantanosas, así como una torre cercana.
Los rectángulos que representan el campo tienen lados opuestos de igual longitud, lo que sugiere que los topógrafos de ese período de tiempo habían ideado una forma de crear líneas perpendiculares con mayor precisión que antes, según Mansfield.
“Al igual que lo haríamos hoy, hay individuos privados que intentan averiguar dónde están sus límites terrestres, y el topógrafo sale, pero en lugar de usar un equipo de GPS, usan triples pitagóricos”.
Aunque Plimpton 322 y Si.427 ambos usan triples pitagóricos, son anteriores al matemático griego Pitágoras en más de 1,000 años.
“Una vez que comprenda qué son las triples pitagóricas, su sociedad habrá alcanzado un nivel particular de sofisticación matemática”, dijo Mansfield.
Los babilonios usaban un sistema numérico de base 60, similar a cómo llevamos el tiempo hoy en día, lo que dificultaba el trabajo con números primos mayores que cinco.
Si.427, fue descrito en la revista Foundations of Science.
“Nadie esperaba que los babilonios estuvieran usando triples pitagóricos de esta manera”, dijo Mansfield. “Es más parecido a las matemáticas puras, inspirado en los problemas prácticos de la época”.
Fuente: The Guardian y UNSW










